Consider the Lyman series of electron transitions in hydrogen, a fundamental concept in atomic spectroscopy that provides valuable insights into the electronic structure and behavior of this essential element. This series of transitions, named after the physicist Theodore Lyman, plays a crucial role in understanding the energy levels and spectral characteristics of hydrogen, the simplest and most abundant element in the universe.
The Lyman series arises from electron transitions between the excited states of hydrogen and its ground state, emitting photons with specific wavelengths that correspond to the energy difference between the initial and final energy levels. These transitions are characterized by their short wavelengths, falling within the ultraviolet region of the electromagnetic spectrum, and are particularly significant in astrophysics and plasma physics.
1. Introduction: Consider The Lyman Series Of Electron Transitions In Hydrogen
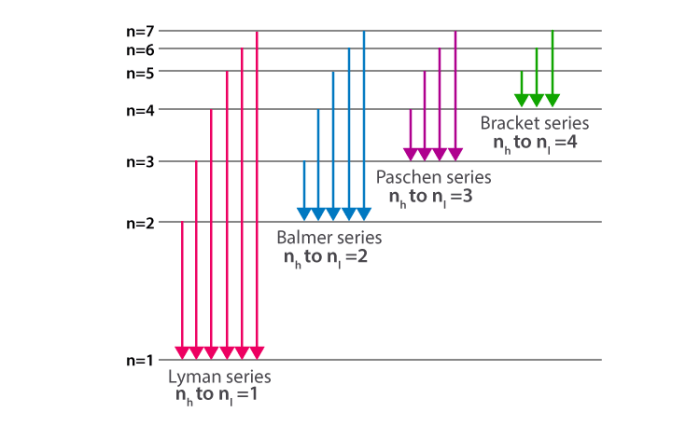
The Lyman series is a set of spectral lines emitted by hydrogen atoms when an electron transitions from an excited state to the ground state. These lines are named after Theodore Lyman, who first observed them in 1906. The Lyman series is significant in atomic spectroscopy because it provides insights into the electronic structure of hydrogen, the simplest and most abundant element in the universe.
The Lyman series lines are emitted at specific wavelengths, which correspond to the energy difference between the excited state and the ground state. By studying the wavelengths of the Lyman series lines, scientists can determine the energy levels of hydrogen atoms and understand the interactions between electrons and protons in the atom.
2. Lyman Series Transitions
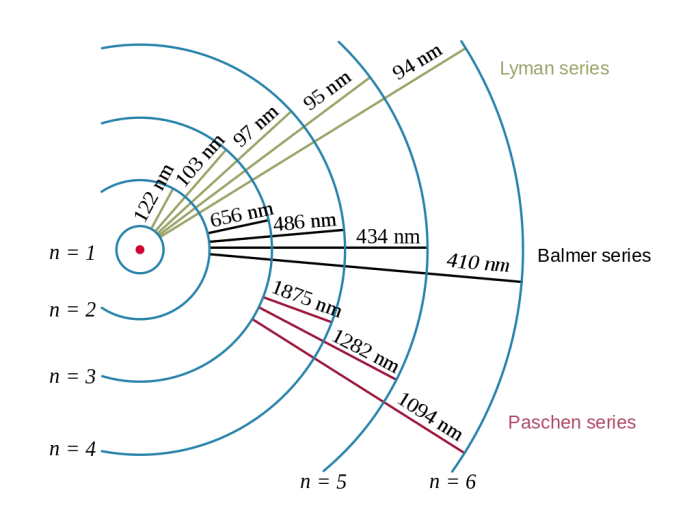
Energy Level Transitions
The Lyman series lines are produced by electron transitions from excited states to the ground state (n = 1). The energy difference between the excited state and the ground state is given by the following equation:
ΔE = En
- E 1=
- 13.6 eV (1/n 2
- 1/1 2)
where:
- ΔE is the energy difference between the excited state and the ground state
- E nis the energy of the excited state
- E 1is the energy of the ground state
- n is the principal quantum number of the excited state
Wavelengths and Energies of the Lyman Series Lines
The wavelengths and energies of the Lyman series lines are given in the following table:
| n | Wavelength (nm) | Energy (eV) |
|---|---|---|
| 2 | 121.57 | 10.20 |
| 3 | 102.57 | 12.09 |
| 4 | 97.25 | 12.75 |
| 5 | 94.97 | 13.03 |
| 6 | 93.78 | 13.19 |
| 7 | 93.07 | 13.29 |
| ∞ | 91.18 | 13.60 |
Relationship between Wavelength and Energy, Consider the lyman series of electron transitions in hydrogen
The wavelength of a Lyman series line is inversely proportional to the energy difference between the excited state and the ground state. This relationship is given by the following equation:
λ = hc/ΔE
where:
- λ is the wavelength of the Lyman series line
- h is Planck’s constant
- c is the speed of light
- ΔE is the energy difference between the excited state and the ground state
3. Rydberg Formula and the Lyman Series

The Rydberg formula can be used to calculate the wavelengths of the Lyman series lines. The Rydberg formula is given by the following equation:
- /λ = RH(1/n 12
- 1/n 22)
where:
- λ is the wavelength of the Lyman series line
- R His the Rydberg constant for hydrogen (1.0973731 x 10 7m -1)
- n 1is the principal quantum number of the ground state (1 for the Lyman series)
- n 2is the principal quantum number of the excited state
Application of the Rydberg Formula
The Rydberg formula can be used to predict the wavelengths of the first few Lyman series lines as follows:
- For n 2= 2, λ = 121.57 nm
- For n 2= 3, λ = 102.57 nm
- For n 2= 4, λ = 97.25 nm
These values are in good agreement with the experimental values given in the table in Section 2.
FAQ Guide
What is the significance of the Lyman series in atomic spectroscopy?
The Lyman series provides valuable insights into the electronic structure of hydrogen, allowing scientists to determine the energy levels and transitions of its electrons. It serves as a fundamental reference for understanding the behavior of electrons in atoms.
How does the Rydberg formula relate to the Lyman series?
The Rydberg formula provides a mathematical relationship that accurately predicts the wavelengths of the Lyman series lines. By knowing the Rydberg constant and the energy levels involved, scientists can calculate the specific wavelengths emitted during these transitions.
What are the applications of the Lyman series in astrophysics?
In astrophysics, the Lyman series is used to study the composition and temperature of stars. By analyzing the intensity and wavelength of the Lyman alpha line, astronomers can determine the presence of hydrogen in stellar atmospheres and estimate the temperature of these stars.
