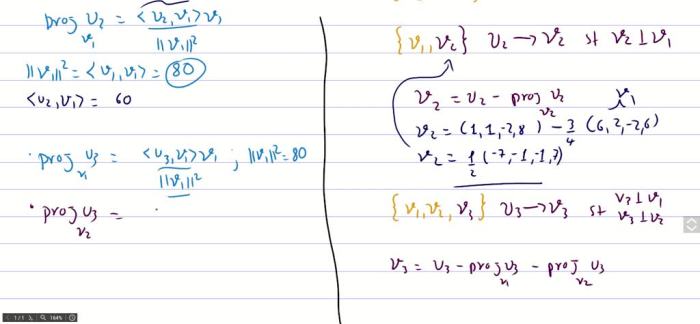Find an orthonormal basis of the row space of a – Finding an orthonormal basis of the row space of a matrix is a fundamental concept in linear algebra. It provides a set of linearly independent vectors that span the row space of the matrix, and these vectors are orthogonal to each other, making them easy to work with.
This concept has applications in various fields, including computer graphics, signal processing, and statistics.
To find an orthonormal basis for the row space of a matrix, we can use the Gram-Schmidt process or the QR decomposition. Both methods involve orthogonalizing the rows of the matrix and normalizing them to have unit length.
Orthogonal and Orthonormal Bases: Find An Orthonormal Basis Of The Row Space Of A

An orthogonal basis for a vector space is a set of vectors that are all mutually orthogonal, meaning that the dot product of any two vectors in the set is zero. An orthonormal basis is an orthogonal basis in which all the vectors have unit length.
The difference between an orthogonal basis and an orthonormal basis is that the vectors in an orthonormal basis are all unit length, while the vectors in an orthogonal basis are not necessarily unit length.
Row Space of a Matrix
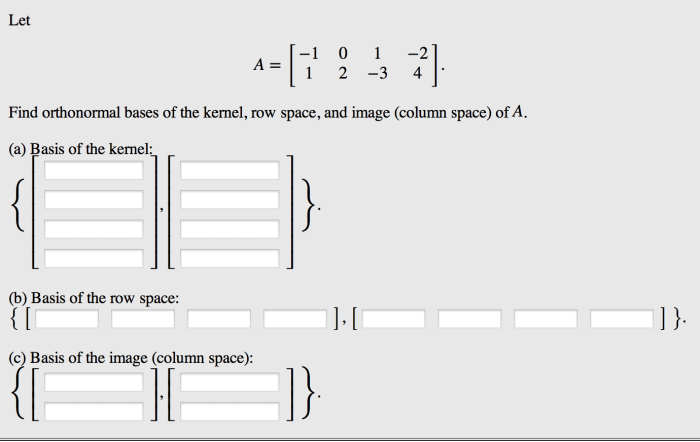
The row space of a matrix is the subspace of the vector space spanned by the rows of the matrix. In other words, the row space of a matrix is the set of all linear combinations of the rows of the matrix.
To find the row space of a matrix, we can use the following steps:
- Row reduce the matrix to echelon form.
- The nonzero rows of the echelon form are a basis for the row space of the matrix.
For example, the row space of the matrix $$\beginbmatrix 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \endbmatrix$$ is the subspace of $\mathbbR^3$ spanned by the vectors $$\beginbmatrix 1 \\ 4 \\ 7 \endbmatrix, \beginbmatrix 2 \\ 5 \\ 8 \endbmatrix.$$
Finding an Orthonormal Basis for the Row Space of a Matrix
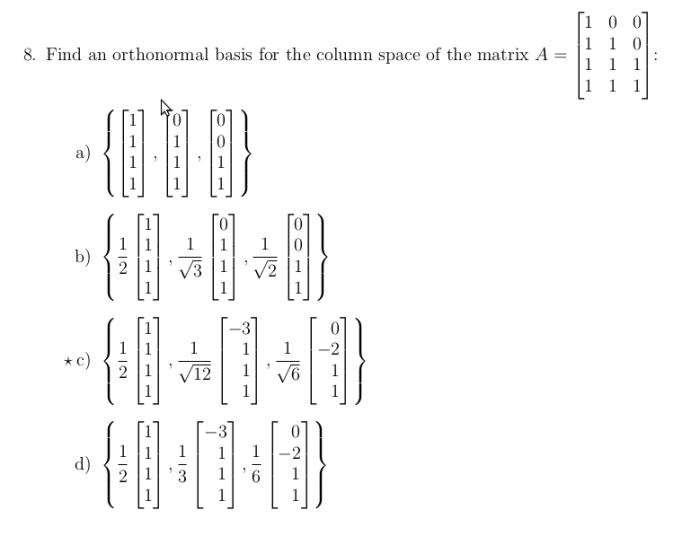
To find an orthonormal basis for the row space of a matrix, we can use the Gram-Schmidt process or the QR decomposition.
The Gram-Schmidt process is an algorithm that takes a set of vectors and orthogonalizes them, and then normalizes them to have unit length. The QR decomposition is a factorization of a matrix into the product of an orthogonal matrix and an upper triangular matrix.
The columns of the orthogonal matrix form an orthonormal basis for the row space of the original matrix.
For example, to find an orthonormal basis for the row space of the matrix $$\beginbmatrix 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \endbmatrix$$ we can use the Gram-Schmidt process to orthogonalize the rows of the matrix and then normalize them to have unit length.
This gives us the following orthonormal basis for the row space of the matrix: $$\beginbmatrix \frac1\sqrt14 & \frac2\sqrt14 & \frac3\sqrt14 \\ \frac4\sqrt58 & \frac5\sqrt58 & \frac6\sqrt58 \\ \frac7\sqrt112 & \frac8\sqrt112 & \frac9\sqrt112 \endbmatrix.$$
Gram-Schmidt Process
The Gram-Schmidt process is an algorithm that takes a set of vectors and orthogonalizes them, and then normalizes them to have unit length. The algorithm works as follows:
- Let $v_1$ be the first vector in the set.
- For each vector $v_i$ in the set, do the following:
- Let $w_i = v_i- \sum_j=1^i-1 \fracv_i \cdot v_jv_j \cdot v_j v_j$.
- Let $u_i = \fracw_i||w_i||$.
The vectors $u_1, u_2, \ldots, u_n$ form an orthonormal basis for the subspace spanned by the original set of vectors.
QR Decomposition, Find an orthonormal basis of the row space of a
The QR decomposition is a factorization of a matrix into the product of an orthogonal matrix and an upper triangular matrix. The QR decomposition can be used to find an orthonormal basis for the row space of a matrix.
The QR decomposition works as follows:
- Let $A$ be an $m \times n$ matrix.
- Let $Q$ be an $m \times m$ orthogonal matrix and $R$ be an $m \times n$ upper triangular matrix such that $A = QR$.
The columns of $Q$ form an orthonormal basis for the row space of $A$.
FAQ Explained
What is the difference between an orthogonal basis and an orthonormal basis?
An orthogonal basis is a set of vectors that are orthogonal to each other, while an orthonormal basis is a set of orthogonal vectors that also have unit length.
How can I find an orthonormal basis for the row space of a matrix?
You can use the Gram-Schmidt process or the QR decomposition to find an orthonormal basis for the row space of a matrix.
What are the applications of finding an orthonormal basis for the row space of a matrix?
Finding an orthonormal basis for the row space of a matrix has applications in computer graphics, signal processing, and statistics.