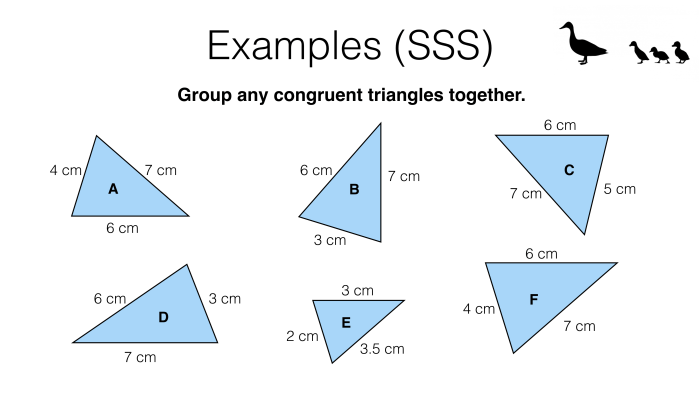Congruent triangles sss and sas worksheet answers – Embark on a journey into the realm of congruent triangles, delving into the intricacies of the Side-Side-Side (SSS) and Side-Angle-Side (SAS) Congruence Theorems. This comprehensive guide unravels the mysteries of congruent triangles, equipping you with a profound understanding of their properties, applications, and the limitations that govern their existence.

Unveiling the intricacies of congruent triangles, this exploration delves into the depths of their properties, limitations, and real-world applications. Prepare to unravel the secrets that lie within the realm of geometry as we embark on this captivating journey.

Congruent Triangles

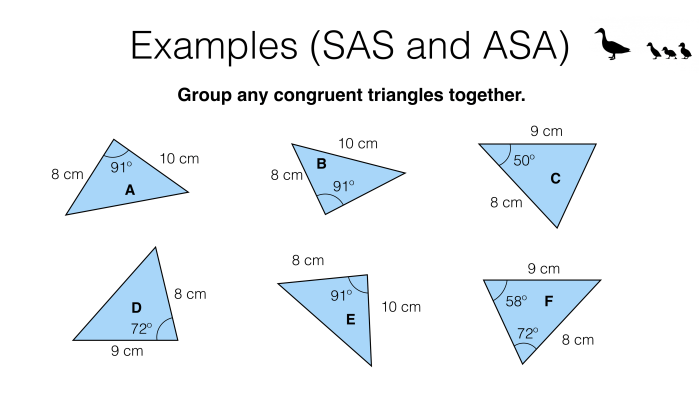
Congruent triangles are triangles that have the same shape and size. They have equal corresponding sides and equal corresponding angles.

Side-Side-Side (SSS) Congruence Theorem, Congruent triangles sss and sas worksheet answers

The SSS Congruence Theorem states that if three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.

For example, if triangle ABC has sides AB = 5 cm, BC = 6 cm, and AC = 7 cm, and triangle DEF has sides DE = 5 cm, EF = 6 cm, and DF = 7 cm, then triangles ABC and DEF are congruent by the SSS Congruence Theorem.

The SSS Congruence Theorem is limited to triangles that have all three sides congruent. It does not apply to triangles that have only two sides congruent.

Side-Angle-Side (SAS) Congruence Theorem

The SAS Congruence Theorem states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.

For example, if triangle ABC has sides AB = 5 cm, BC = 6 cm, and angle B = 60 degrees, and triangle DEF has sides DE = 5 cm, EF = 6 cm, and angle D = 60 degrees, then triangles ABC and DEF are congruent by the SAS Congruence Theorem.

The SAS Congruence Theorem is limited to triangles that have two sides and the included angle congruent. It does not apply to triangles that have only one side and one angle congruent.

Worksheet Answers

Problem 1:Use the SSS Congruence Theorem to determine if triangles ABC and DEF are congruent.

Given:AB = 5 cm, BC = 6 cm, AC = 7 cm, DE = 5 cm, EF = 6 cm, DF = 7 cm

Solution:Since all three sides of triangle ABC are congruent to the corresponding sides of triangle DEF, the triangles are congruent by the SSS Congruence Theorem.

Problem 2:Use the SAS Congruence Theorem to determine if triangles ABC and DEF are congruent.

Given:AB = 5 cm, BC = 6 cm, angle B = 60 degrees, DE = 5 cm, EF = 6 cm, angle D = 60 degrees

Solution:Since two sides and the included angle of triangle ABC are congruent to the corresponding sides and angle of triangle DEF, the triangles are congruent by the SAS Congruence Theorem.

Applications of Congruent Triangles

Congruent triangles have many applications in real-world situations.

• Architecture:Congruent triangles are used to design and construct symmetrical buildings and structures.
• Engineering:Congruent triangles are used to design and build bridges, airplanes, and other structures that require precise measurements.
• Design:Congruent triangles are used to create patterns and designs in art, fashion, and interior design.

Understanding congruence is essential for success in various disciplines, including geometry, engineering, and architecture.

FAQ Explained: Congruent Triangles Sss And Sas Worksheet Answers

What is the SSS Congruence Theorem?

The SSS Congruence Theorem states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

What is the SAS Congruence Theorem?

The SAS Congruence Theorem states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

What are the limitations of the SSS and SAS Congruence Theorems?

The SSS and SAS Congruence Theorems only apply to triangles. They do not apply to other geometric shapes, such as quadrilaterals or circles.