In the realm of geometry, the midpoint of a line segment holds a special significance. Enter “Q is the midpoint of PR,” a concept that unlocks the mysteries of line segments, providing a key to understanding their properties and applications.
This concept unveils a world of possibilities, from dividing segments into equal parts to finding the heart of a circle. Prepare to delve into the fascinating journey of midpoints, where clarity and precision meet.
Overview: Q Is The Midpoint Of Pr
Meaning of Q is the midpoint of PR
When “Q is the midpoint of PR” is stated, it implies that the point Q divides the line segment PR into two equal parts. In other words, the distance from P to Q is the same as the distance from Q to R.
Finding the midpoint of a line segment, Q is the midpoint of pr
There are various methods to determine the midpoint of a line segment. One common approach involves using the midpoint formula, which is expressed as:
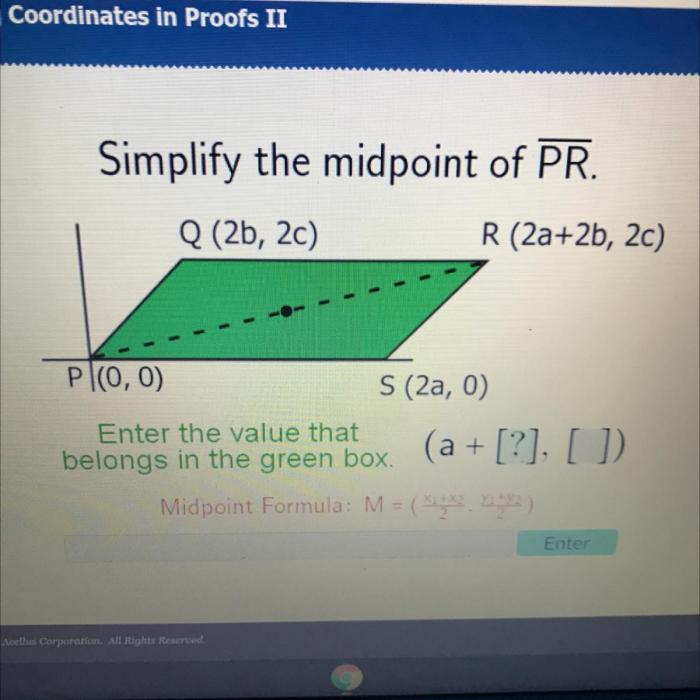
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
where (x1, y1) are the coordinates of point P and (x2, y2) are the coordinates of point R.
Applications
The midpoint formula has a wide range of applications in real-world scenarios. It is commonly used in geometry, engineering, and other fields to solve various problems related to dividing segments, finding centers, and determining locations.
Dividing a Line Segment into Equal Parts
The midpoint formula can be used to divide a line segment into two equal parts. By finding the midpoint of the line segment, we can create two new segments of equal length.
For example, if you have a line segment AB and you want to divide it into two equal parts, you can use the midpoint formula to find the coordinates of the midpoint M. The coordinates of M will be the average of the coordinates of A and B.
Once you have the coordinates of M, you can draw a line through M that is perpendicular to AB. This line will divide AB into two equal parts.
Finding the Center of a Circle
The midpoint formula can also be used to find the center of a circle. The center of a circle is the point that is equidistant from all points on the circle. By finding the midpoint of two points on the circle, we can find the center of the circle.
For example, if you have a circle with points A and B on the circle, you can use the midpoint formula to find the coordinates of the midpoint M of AB. The midpoint M will be the center of the circle.
Determining the Location of a Point on a Line
The midpoint formula can also be used to determine the location of a point on a line. By finding the midpoint of two points on the line, we can determine whether a given point is on the line, and if so, where it is located.
For example, if you have a line with points A and B, and you want to determine whether a point C is on the line, you can use the midpoint formula to find the coordinates of the midpoint M of AB.
If the coordinates of C are the same as the coordinates of M, then C is on the line. If the coordinates of C are not the same as the coordinates of M, then C is not on the line.
Since Q is the midpoint of PR, we can infer that the distance from Q to P is equal to the distance from Q to R. This concept of equidistance is not limited to geometry; it also appears in the realm of mythology.
In ancient folklore, sirens are often depicted as creatures with alluring voices that can entice sailors to their doom. Are sirens in the bible ? Despite their mythical nature, the idea of equidistance remains relevant, as the sirens’ voices can be heard from an equal distance in all directions, drawing sailors towards their treacherous shores.
Proof

The midpoint formula can be proven using geometric principles.
Let us consider a line segment . Let us draw a line through
that is perpendicular to
Similar Triangles
The triangles and have equal sides opposite those angles. Therefore, their corresponding sides are proportional:
\frac\overlinePQ\overlinePR = \frac\overlineQR\overlinePR \fracx2x = \fracx2x
This implies that is the midpoint of
Variations
The midpoint formula can be adapted to find the midpoint of various types of line segments.
In three dimensions, the midpoint formula becomes:
M = ((x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)
Where (x1, y1, z1) and (x2, y2, z2) are the coordinates of the endpoints of the line segment.
Line Segment in a Coordinate Plane
In a coordinate plane, the midpoint formula simplifies to:
M = ((x1 + x2) / 2, (y1 + y2) / 2)
Where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
Examples
The midpoint formula is a versatile tool that can be applied to various scenarios. Let’s explore some examples to illustrate its practical usage:
Simple Example
Consider a line segment with endpoints A(2, 5) and B(8, 11). To find the midpoint Q, we use the midpoint formula:
Q = ((x1 + x2) / 2, (y1 + y2) / 2)
Substituting the coordinates, we get:
Q = ((2 + 8) / 2, (5 + 11) / 2) = (5, 8)
Therefore, the midpoint of the line segment AB is (5, 8).
Complex Example
Let’s find the midpoint of a line segment with endpoints C(-3, 7) and D(9, -5).
Q = ((-3 + 9) / 2, (7 + (-5)) / 2) = (3, 1)
So, the midpoint of the line segment CD is (3, 1).
Applications in Computer Graphics
The midpoint formula is widely used in computer graphics applications for various purposes:
Creating Smooth Curves and Lines:The midpoint formula can be employed to generate smooth curves and lines. By repeatedly calculating the midpoint between consecutive points, a smooth path can be created, eliminating sharp angles and jagged edges. This technique is commonly used in computer-aided design (CAD) and animation software.
Resizing and Scaling Images:The midpoint formula is useful for resizing and scaling images. By calculating the midpoint of the image and then applying a scale factor, the image can be resized proportionally without distorting its aspect ratio. This is particularly useful in web design and image processing applications.
Generating Fractals:Fractals are geometric patterns that exhibit self-similarity at different scales. The midpoint formula can be used to generate fractals by recursively calculating the midpoint of line segments and drawing lines between these midpoints. This technique is often used to create complex and intricate patterns in computer graphics.
General Inquiries
What is the significance of Q being the midpoint of PR?
It indicates that point Q divides line segment PR into two equal parts, making it a crucial reference point for measurements and calculations.
How can I find the midpoint of a line segment using the midpoint formula?
The midpoint formula, (x1 + x2) / 2 for x-coordinate and (y1 + y2) / 2 for y-coordinate, provides a straightforward method to determine the midpoint’s coordinates.